Complete Guide to Trigonometric Ratios and Identities

Trigonometry is a part of mathematics that helps us understand angles and sides of triangles. At first, it may look difficult, but when learned step by step, it becomes easy and interesting. Trigonometric ratios help students measure heights, distances, and angles using simple formulas. In this guide, you will learn trigonometric ratios, identities, formulas, and solved examples in a clear and simple way. This will help you build strong basics and feel more confident in math by Mixt Academy’s online maths tutors.

Table of Contents

Add a header to begin generating the table of contents

What is Trigonometry?

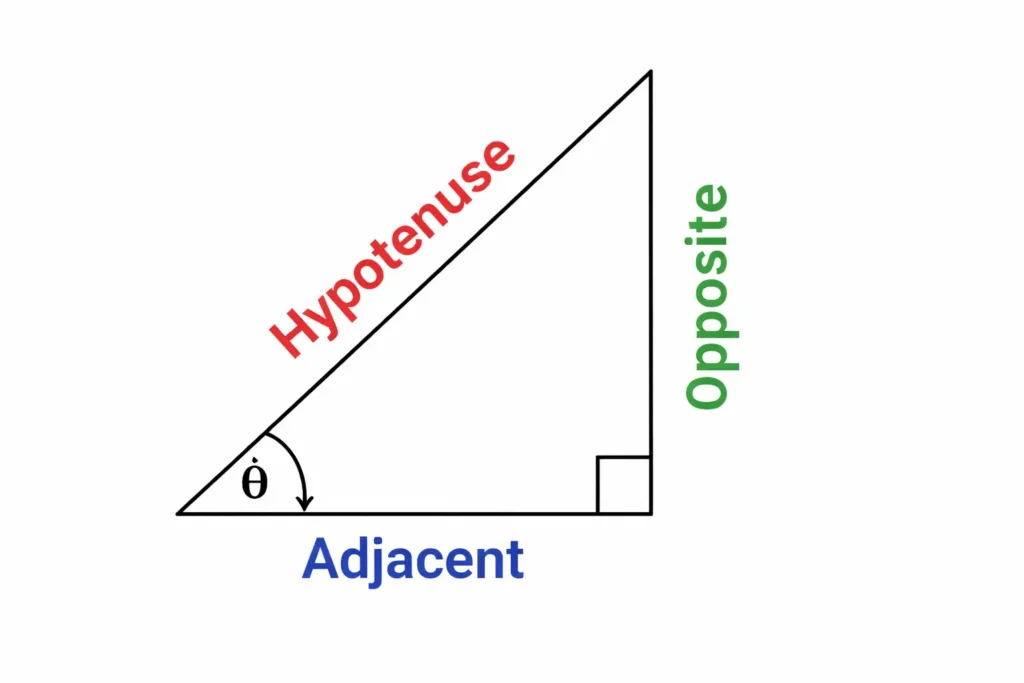
Trigonometric ratios are right-angled triangle functions that show the relationship between angles and sides.

Topics Trigonometry Covers

The following are the topics trigonometry covers:

Right Triangle Trigonometry
Unit Circle
Graphs of Trig Functions
Trigonometric Identities
Inverse Trig Functions
Solving Triangles
Trigonometric Equations
Real World Applications

What Skills Does Trigonometry Develop?

Trigonometry in Mathematics develops core skills like problem-solving abilities, logical and analytical thinking, a strong foundation of advanced mathematics, critical thinking, and spatial reasoning.

What are Trigonometric Ratios?

If we have a right-angle triangle, the length of each side of the triangle tells how steep or wide the given angle is, and trigonometric ratios are the simple comparison of those side lengths of the angle. The basic trigonometric ratios include sine, cosine, and tangent. However, other trigonometric ratios include cosec, sec, and cot.

How to Find Trigonometric Ratios?

In a right-angle triangle (an angle = 90°), find out

Opposite: The side opposite to θ
Adjacent: The side next to θ
Hypotenuse: The side always opposite the right angle

Identifying adjacent, opposite and hypotenuse will help you find trigonometric ratios.

Trigonometric Ratio Formulas

sin θ = opposite/hypotenuse
cos θ = adjacent/hypotenuse
tan θ = opposite/adjacent

For Example

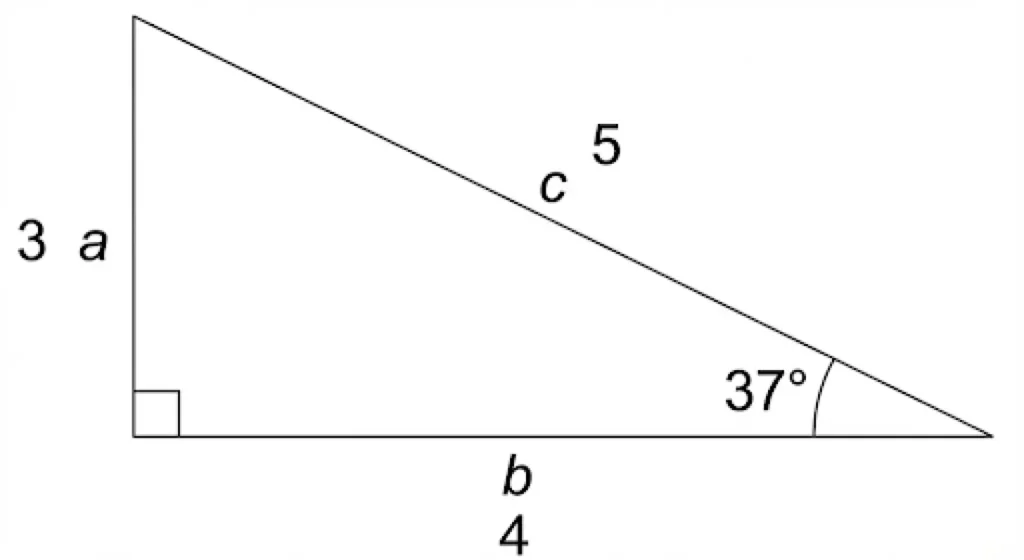
In the above given right-angle triangle

c = Hypotenuse = 5

a = Opposite = 3

b = Adjacent = 4

The trigonometric ratios for the above right-angle triangle will be

sin (37°) = opposite/hypotenuse = 3/5

cos (37°) = adjacent/hypotenuse = 4/5

tan θ = opposite/adjacent = 3/4

Confused by Trig Ratios? Get Help Now

Learn sine, cosine, and tangent easily with one-on-one tutor support.

Book a Free Trial Class

SOH-CAH-TOA Technique

SOH-CAH-TOA is a simple way to learn how to memorize trigonometric ratios without confusion.

SOH means: Sine = Opposite / Hypotenuse
CAH means: Cosine = Adjacent / Hypotenuse
TOA means: Tangent = Opposite / Adjacent

How to Find Trigonometric Ratios?

Besides the core three sine, cosine and tangent, other trigonometric ratios include Cotangent, Secant, and Cosecant.

As we know how to find hypotenuses, perpendicular or opposite (same), and adjacent, it will be easy to find all trig ratios. The following are the formulas to find other trigonometric ratios.

Sine = sin θ = opposite/hypotenuse
Cosine = cos θ = adjacent/hypotenuse
Tangent = tan θ = opposite/adjacent
Cosecant = cscθ = Hypothesis/Opposite
Secant = secθ =Hypothesis/Adjacent
Cotangent = cot θ = Adjacent/Opposite

For Example

In Figure 1.2, the given sides are

Hypotenuse = 5

Opposite = 3

Adjacent = 4

So the trigonometry ratios will be

sin θ = opposite/hypotenuse = 3/5

cos θ = adjacent/hypotenuse = 4/5

tan θ = opposite/adjacent = 3/4

cscθ = Hypothesis/Opposite = 5/3

secθ = Hypothesis/Adjacent = 5/4

cot θ = Adjacent/Opposite = 4/3

All Trigonometric Ratios Formulas

Below is a cleaner look at all trigonometric ratios with their formulas. Students can practice using a trigonometric ratios formula worksheet to strengthen their understanding.

Trigonometric Ratios Table

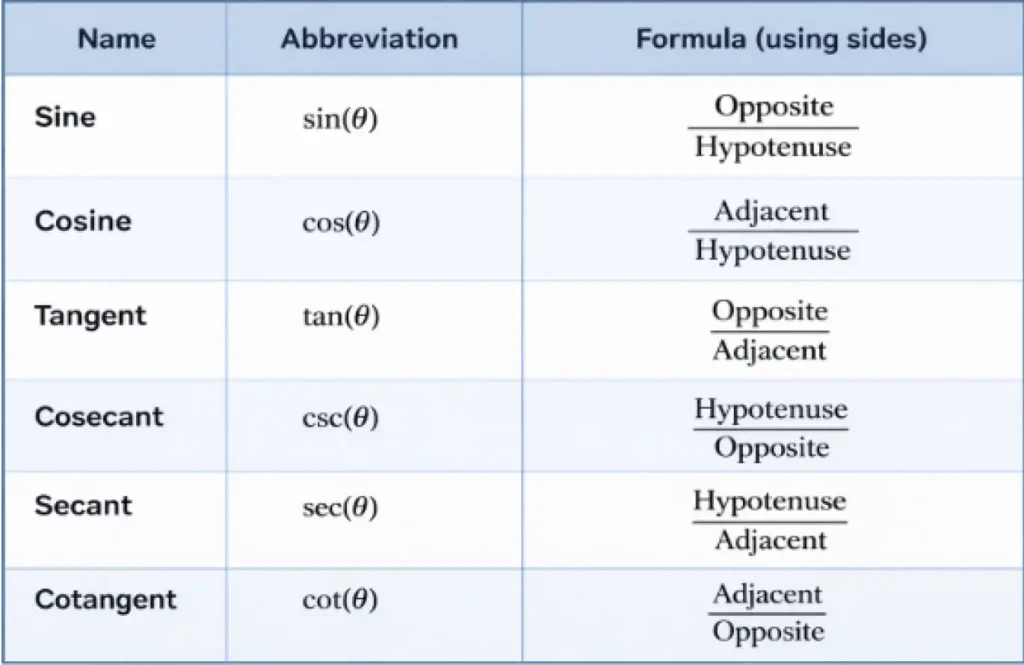
Below is the trigonometric ratios table with respect to angles 0°, 30°, 45°, 60°, and 90°.

θ (degrees)	sin θ	cos θ	tan θ	cosec θ	sec θ	cot θ
0°	0	1	0	Not defined	1	Not defined
30°	1/2	√3/2	1/√3	2	2/√3	√3
45°	1/√2	1/√2	1	√2	√2	1
60°	√3/2	1/2	√3	2/√3	2	1/√3
90°	1	0	Not defined	1	Not defined	0

Trigonometric Identities

Trigonometric identities are true for every value of the variable recurring on both sides of the expression or equation. Trigonometric identities involve all trigonometric functions (sine, cosine, tangent, secant, cosecant, and cotangent. Trigonometric identities include:

sin²θ + cos²θ = 1
1 + tan²θ = sec²θ
1 + cot²θ = cosec²θ
tan θ = sin θ / cos θ
cot θ = cos θ / sin θ

Difference Between Trig Ratios and Trig Identities

Trigonometric Ratios	Trigonometric Identities
Defined using triangle sides	Equations always true
Depend on a right-angled triangle	Independent of the triangle
Used to find values	Used to simplify & prove
Example: sin θ = opp/hyp	Example: sin²θ + cos²θ = 1

Fundamental Trigonometric Identities

Below are common trigonometric identities used to solve complex maths problems.

Reciprocal Identities

sin θ = 1 / cosec θ
cosec θ = 1 / sin θ
cos θ = 1 / sec θ
sec θ = 1 / cos θ
tan θ = 1 / cot θ
cot θ = 1 / tan θ

Quotient Identities

tan θ = sin θ / cos θ
cot θ = cos θ / sin θ

Pythagorean Trig Identities

sin²θ + cos²θ = 1
1 + tan²θ = sec²θ
1 + cot²θ = cosec²θ

Double-Angle Trigonometric Identities

Sine

sin 2θ = 2 sin θ cos θ

Cosine

cos 2θ = cos²θ − sin²θ
cos 2θ = 1 − 2 sin²θ
cos 2θ = 2 cos²θ − 1

Tangent

tan 2θ = 2 tan θ / (1 − tan²θ)

Cotangent

cot 2θ = (cot²θ − 1) / (2 cot θ)

Half-Angle Trigonometric Identities

Sine

sin(θ/2) = ± √[(1 − cos θ) / 2]

Cosine

cos(θ/2) = ± √[(1 + cos θ) / 2]

Tangent

tan(θ/2) = ± √[(1 − cos θ) / (1 + cos θ)]
tan(θ/2) = (1 − cos θ) / sin θ
tan(θ/2) = sin θ / (1 + cos θ)

Cotangent

cot(θ/2) = ± √[(1 + cos θ) / (1 − cos θ)]
cot(θ/2) = (1 + cos θ) / sin θ
cot(θ/2) = sin θ / (1 − cos θ)

Sum and Difference Trigonometric Identities

Sine

sin(A + B) = sin A cos B + cos A sin B
sin(A − B) = sin A cos B − cos A sin B

Cosine

cos(A + B) = cos A cos B − sin A sin B
cos(A − B) = cos A cos B + sin A sin B

Tangent

tan(A + B) = (tan A + tan B) / (1 − tan A tan B)
tan(A − B) = (tan A − tan B) / (1 + tan A tan B)

Product-to-Sum Trigonometric Identities

Sine × Sine

sin A sin B = ½ [cos(A − B) − cos(A + B)]

Cosine × Cosine

cos A cos B = ½ [cos(A − B) + cos(A + B)]

Sine × Cosine

sin A cos B = ½ [sin(A + B) + sin(A − B)]
cos A sin B = ½ [sin(A + B) − sin(A − B)]

Sum-to-Product Identities

Sine

sin A + sin B = 2 sin((A + B)/2) cos((A − B)/2)
sin A − sin B = 2 cos((A + B)/2) sin((A − B)/2)

Cosine

cos A + cos B = 2 cos((A + B)/2) cos((A − B)/2)
cos A − cos B = −2 sin((A + B)/2) sin((A − B)/2)

Triple-Angle Identities

Sine

sin 3θ = 3 sin θ − 4 sin³θ

Cosine

cos 3θ = 4 cos³θ − 3 cos θ

Tangent

tan 3θ = (3 tan θ − tan³θ) / (1 − 3 tan²θ)

Power-Reduction (Reduction) Identities

sin²θ = (1 − cos 2θ) / 2
cos²θ = (1 + cos 2θ) / 2
tan²θ = (1 − cos 2θ) / (1 + cos 2θ)

Co-Function Identities

sin(90° − θ) = cos θ
cos(90° − θ) = sin θ
tan(90° − θ) = cot θ
sec(90° − θ) = cosec θ
cosec(90° − θ) = sec θ
cot(90° − θ) = tan θ

Negative-Angle Identities

sin(−θ) = −sin θ
cos(−θ) = cos θ
tan(−θ) = −tan θ

Periodic Identities

sin(θ + 2π) = sin θ
cos(θ + 2π) = cos θ
tan(θ + π) = tan θ

Improve Your Trig Exam Scores

Get personalised feedback and fix mistakes before your next test.

Book a Free Trial Class

Trigonometry Solved Questions Samples

Question 1: Find the value

If sin θ = 3/5, where θ is acute, find cos θ and tan θ.

Solution:

Given:
sin θ = Opposite / Hypotenuse = 3/5

So:
Opposite = 3
Hypotenuse = 5

Using Pythagoras:
Adjacent = √(5² − 3²)
Adjacent = √(25 − 9) = √16 = 4

Now:

cos θ = Adjacent / Hypotenuse = 4/5
tan θ = Opposite / Adjacent = 3/4

Answer:
cos θ = 4/5
tan θ = 3/4

Question 2: Evaluate

sin 30° + cos 60°

Solution:

We know:

sin 30° = 1/2
cos 60° = 1/2

So:
sin 30° + cos 60° = 1/2 + 1/2 = 1

Answer: 1

Question 3: Prove that

(1 − cos 2θ) / sin 2θ = tan θ

Solution:

(1 − cos 2θ) / sin 2θ

= (2 sin²θ) / (2 sin θ cos θ)

= sin θ / cos θ

= tan θ

Hence Proved

Question 4: Evaluate

sin θ / (1 + cos θ) + (1 + cos θ) / sin θ

Solution:

sin θ / (1 + cos θ) + (1 + cos θ) / sin θ

= sin²θ / (sin θ(1 + cos θ)) + (1 + cos θ)² / (sin θ(1 + cos θ))

= (sin²θ + (1 + cos θ)²) / (sin θ(1 + cos θ))

= (sin²θ + (1 + 2 cos θ + cos²θ)) / (sin θ(1 + cos θ))

= ((sin²θ + cos²θ) + 1 + 2 cos θ) / (sin θ(1 + cos θ))

= (1 + 1 + 2 cos θ) / (sin θ(1 + cos θ))

= 2(1 + cos θ) / (sin θ(1 + cos θ))

= 2 / sin θ

= 2 cosec θ

Question 4: Evaluate

Simplified Identity

Find the value of 9 csc^2θ − 9 cot^2θ.

Solution:

Factor out 9:

9(csc^2θ − cot^2θ)

Using the identity:

1 + cot^2θ = csc^2θ

So,

csc^2θ − cot^2θ = 1

Therefore:

9(1) = 9

Trigonometry Sample MCQs

1. If sin θ = 3/5, where θ is acute, what is cos θ?

A) 3/4
B) 4/5
C) 5/3
D) 5/4

Correct Answer: B) 4/5

2. Evaluate: sin 30° + cos 60°

A) 0
B) 1/2
C) 1
D) 2

Correct Answer: C) 1

3. Which of the following is equal to 1 + tan²θ?

A) cosec²θ
B) sec²θ
C) cot²θ
D) sin²θ

Correct Answer: B) sec²θ

4. Find the value of: (sec θ − tan θ)(sec θ + tan θ)

A) 0
B) 1
C) sec²θ
D) tan²θ

Correct Answer: B) 1

5. Evaluate: sin 2θ / (1 + cos 2θ)

A) sin θ
B) cos θ
C) tan θ
D) cot θ

Correct Answer: C) tan θ

How Does Mixt Academy Help Students Excel in Mathematics?

Mixt Academy is providing expert tutors for all subjects, including mathematics. We will note the student’s academic requirement first and then match each student with the most suitable online maths tutors who are connected globally on our platform. Flexible timings and easy-to-understand lectures help students achieve higher grades in tests or exams. So, either you need help with your daily homework, or it’s the IGCSE, GCSE or A level, we provide customised support for all curricula and subjects.

Learn Trigonometry With Expert Tutors

Flexible timings, clear teaching, and personalised math support for students.

Book a Free Trial Class

Mastering Trigonometry Made Easy

Trigonometry may seem challenging at the beginning, but with practice and the right steps, it becomes much easier to understand. By learning trigonometric ratios, formulas, and identities, students can solve many math problems quickly and correctly. Remember to practice regularly, use shortcuts like SOH-CAH-TOA, and understand each step instead of memorising blindly. With time and practice, mastering trigonometric ratios will feel simple and rewarding.

FAQs About Trigonometric Ratios

What are the formulas of trigonometry?

The main trigonometric ratios formulas are as follows.

sin θ = Opposite / Hypotenuse
cos θ = Adjacent / Hypotenuse
tan θ = Opposite / Adjacent
cosec θ = 1 / sin θ
sec θ = 1 / cos θ
cot θ = 1 / tan θ

What are the three most common trigonometric ratios?

The common trigonometric ratios include sine, cosine and tangent.

What are the trigonometric ratios?

Trigonometric ratios deal with the relationship between the angles and side lengths in a right-angle triangle.

What are the 6 trigonometric ratios?

The six trigonometric ratios include the core three ratios, sine, cosine, and tangent, and other ratios include cosecant, secant and cotangent.

What are the 4 parts of trigonometry?

4 parts of trigonometry refer to the four main categories that trigonometry deals with, which include core right-angle triangle, spherical, plane and analytical trigonometry.

Complete Guide to Trigonometric Ratios and Identities

What is Trigonometry?

Topics Trigonometry Covers

What Skills Does Trigonometry Develop?

What are Trigonometric Ratios?

How to Find Trigonometric Ratios?

Trigonometric Ratio Formulas

SOH-CAH-TOA Technique

How to Find Trigonometric Ratios?

All Trigonometric Ratios Formulas

Trigonometric Ratios Table

Trigonometric Identities

Difference Between Trig Ratios and Trig Identities

Fundamental Trigonometric Identities

Reciprocal Identities

Quotient Identities

Pythagorean Trig Identities

Double-Angle Trigonometric Identities

Half-Angle Trigonometric Identities

Sum and Difference Trigonometric Identities

Product-to-Sum Trigonometric Identities

Sum-to-Product Identities

Triple-Angle Identities

Power-Reduction (Reduction) Identities

Co-Function Identities

Negative-Angle Identities

Periodic Identities

Trigonometry Solved Questions Samples

Question 1: Find the value

Question 2: Evaluate

Question 3: Prove that

Question 4: Evaluate

Question 4: Evaluate

Trigonometry Sample MCQs

How Does Mixt Academy Help Students Excel in Mathematics?

Mastering Trigonometry Made Easy

FAQs About Trigonometric Ratios

Mixt Academy

Recently posts

Categories

IGCSE Popular Blogs

GCSE Popular Blogs

AS & A Level Popular Blogs

IB Popular Blogs

OCR Popular Blogs

AQA Popular Blogs

UAE Office

UK Office